在高中，我们学过正弦函数，也知道一些特殊角度的正弦数值，如sin90°=1，sin60°=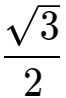

，sin45°=，sin30°=0.5。但是对于其他非特殊角度的正弦值，我们就不太好计算了。

最近，我在图书馆看到一本国外的科普书《天啊，几何还能这样学》，里面就聊到如何快速手算任意角度的正弦值，以及如何根据正弦值求解角度。里面介绍的方法很新颖，也很有效果，如下图所示：

这种方法的原理是，当角度很小时，该角度所对的圆弧与半径的比值与正弦值非常接近，误差很小。这时，计算正弦值就转换为计算圆弧与半径的比值。

如下图所示，点A为圆心，AB、AD为圆的半径，BD是角A所对应的圆弧，BC垂直AD于C。当角A很小时，圆弧BD与线段BC的长度就非常接近。

假设AB=R，于是sinA°=BC/ABBD/AB=BD/R。

又因为BD=2R（A/360），于是sinA°BD/R=（A/360）=A/180。

当已知正弦值需要求角度时，A180*sinA°/。

从中，我们可以看出来，当角度很小时，正弦值与角度接近成正比，利用这个特征，我们就能够根据角度求解正弦值，以及根据正弦值求解角度。

一、求sin1°~sin15°以及正弦值为0~0.259时对应的角度。

因为sinA°BD/R=2（A/360）=A/180，于是：

1、sin1°=1*/180=0.01745。

（查正弦表可知，sin1°=0.01745……，这时两者小数点5位以内数值都是一致的）

2、sin2°=2*/180=0.03491。

（查正弦表可知，sin2°=0.03489……，这时两者小数点3位以内数值都是一致的）

3、sin10°=10*/180=0.17453。

（查正弦表可知，sin10°=0.17364……，这时两者小数点2位以内数值都是一致的）

4、sin15°=15*/180=0.26180。

（查正弦表可知，sin15°=0.25881……，这时两者小数点1位以内数值都是一致的，这时误差为（0.26180-0.25881）/0.25881=1.15%，这个误差还是相对比较小的，属于可接受范围。）

于是当正弦值已知，且小于0.26时，我们就可以利用A180*sinA°/这个公式快速求出角度，下面我举几个例子：

5、当正弦值为0.25时，这时我们要求的角度A180*sinA°/=180*0.25/=14.32°。

6、当正弦值为0.2时，这时我们要求的角度A180*sinA°/=180*0.2/=11.46°。

7、当正弦值为0.1时，这时我们要求的角度A180*sinA°/=180*0.1/=5.73°。

8、当正弦值为0.08时，这时我们要求的角度A180*sinA°/=180*0.08/=4.58°。

二、求sin15°~sin30°以及正弦值为0.259~0.5时对应的角度。

1、sin30°=30*/180=0.52360。

（我们知道sin30°=0.5，这时依据上述方法算出来的误差为（0.52360-0.5）/0.5=4.72%，这个误差已经很大了，是无法接受的。）

2、这时为了降低误差，我们需要利用勾股定理求出15度角的正弦值（sin15°）。

已知AB=AD，AC垂直于BD，角BAC=角DAC=15°，角BAE=30°，BE垂直于AD，于是BC=CD。

因为角BAE=30°，所以BE=AB，AE=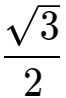AB，ED=AD-AE=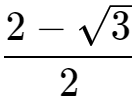AB。

在三角形BED中，。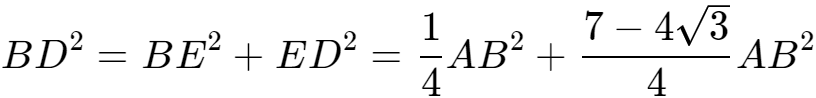

可计算得出：。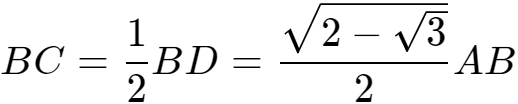

于是sin15°=BC/AB==0.258819……=0.259（取3位小数）

又sin30°=0.5，所以（sin30°-sin15°）/15=0.01608=0.016（取3位小数）

15°~30°，我们认为角度在增加，正弦值也随之成比例增加，即角度每增加1°，正弦值随之增加0.016。

3、于是：

sin15°=0.259

sin16°=0.259+0.016=0.275

……

sin20°=0.259+0.016*5=0.339

（查正弦表可知，sin20°=0.342……，误差很小）

……

sin25°=0.259+0.016*10=0.419

（查正弦表可知，sin25°=0.422……，误差很小）

……

同样地，当正弦值已知，且处在0.259（sin15°）~0.5（sin30°）时，利用前面的结论15°~30°，我们认为角度在增加，正弦值也随之成比例增加，即角度每增加1°，正弦值随之增加0.016，我们可以根据正弦值快速求出相对应的角度：

4、当正弦值为0.3时，这时我们要求的角度A=15+（0.3-0.259）/0.016=17.6°。

5、当正弦值为0.4时，这时我们要求的角度A=15+（0.4-0.259）/0.016=23.8°。

6、当正弦值为0.45时，这时我们要求的角度A=15+（0.45-0.259）/0.016=26.9°。

……

三、求sin30°~sin45°以及正弦值为0.5~0.707时对应的角度。

1、sin30°=0.5，sin45°=（取3位小数）

2、（sin45°-sin30°）/15=0.01608=0.0138=0.014。（取3位小数）

3、30°~45°，我们认为角度在增加，正弦值也随之成比例增加，即角度每增加1°，正弦值随之增加0.014。

4、于是：

sin30°=0.5

sin31°=0.5+0.014=0.514

……

sin35°=0.5+0.014*5=0.570

（查正弦表可知，sin35°=0.5735……，误差很小）

……

sin40°=0.5+0.014*10=0.640

（查正弦表可知，sin40°=0.6427……，误差很小）

……

sin44°=0.5+0.014*14=0.696

（查正弦表可知，sin44°=0.69465……，误差很小）

同样地，当正弦值已知，且处在0.5（sin30°）~0.707（sin45°）时，利用前面的结论30°~45°，我们认为角度在增加，正弦值也随之成比例增加，即角度每增加1°，正弦值随之增加0.014，我们可以根据正弦值快速求出相对应的角度：

5、当正弦值为0.6时，这时我们要求的角度A=30+（0.6-0.5）/0.014=37.1°。

6、当正弦值为0.7时，这时我们要求的角度A=30+（0.7-0.5）/0.014=44.3°。

……

四、求sin45°~sin90°以及正弦值为0.707~1时对应的角度。

1、如下图，在直角三角形ABC中，角C是直角，角A+角B=90°。

2、于是 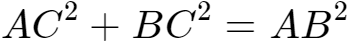：，等式两边同时除以。

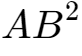3、可得。

4、于是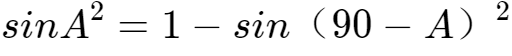

5、于是：sin46°=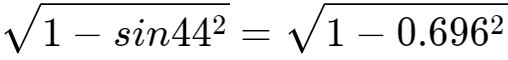=0.718

（查正弦表可知，sin46°=0.71933……，误差很小）

……

sin50°=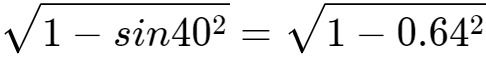=0.768

（查正弦表可知，sin50°=0.76604……，误差很小）

……

sin65°=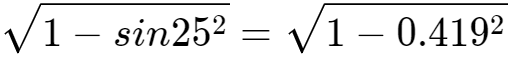=0.908

（查正弦表可知，sin65°=0.90630……，误差很小）

……

sin75°=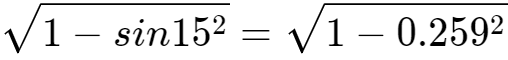=0.966

（查正弦表可知，sin75°=0.96592……，误差很小）

……

sin80°=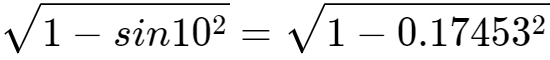=0.985

（查正弦表可知，sin80°=0.98480……，误差很小）

……

6、下面我们根据正弦值求解角度：

根据前面结论：，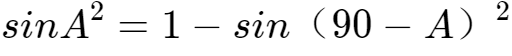

可得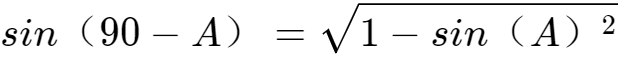

这时，我们就能根据正弦值，快速求解出角度了：

7、当sinA=0.75时，得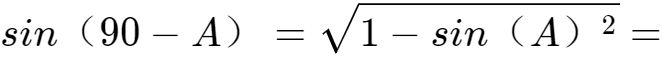0.66，这时0.66处在0.5~0.707之间，90-A=30+（0.66-0.5）/0.014=41.4°，于是A=90-41.4=48.6°。

8、当sinA=0.8时，得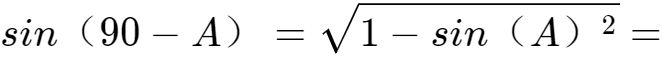0.6，这时0.6处在0.5~0.707之间，90-A=30+（0.6-0.5）/0.014=37.1°，于是A=90-37.1=52.9°。

9、当sinA=0.85时，得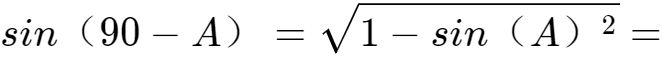0.53，这时0.6处在0.5~0.707之间，90-A=30+（0.53-0.5）/0.014=32.1°，于是A=90-32.1=57.9°。

……

好了，这种方法就介绍到这里了。

我是科学发现之历程，一个致力于科普数学、物理的科技媒体。想了解更多相关的知识，关注微信公众号科学发现之历程，期待你的到来~